Simple Ways to Solve Equations with Infinite Solutions
Before understanding our title topic, let us first know what does an expression and equation mean. Algebra (a subject that involves mathematical symbols and the rules for manipulating these symbols) deals with expressions and equations.
Expression: Expression is like a phrase. It can be a number, a variable, or a combination of both numbers and variables and operation symbols.
Eg: x/y, n-1, 8+2, 4*6
Equation: When an equal symbol connects two expressions, they become an equation.
Eg: y=100, n-1=40, 2+4=6, 7*8=56, 2x+3 = 4 (y+2)
Now let us know,
What is a Linear Equation?
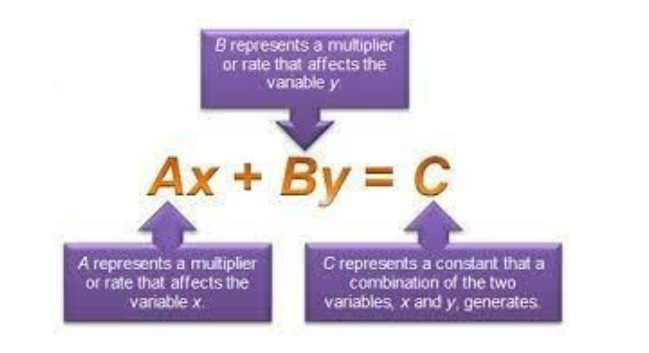
A linear equation is an algebraic equation in which the highest exponent of each variable is one. If a graph is constructed with the equation, it gives a straight line. Standard expression of linear equation is : a1x1+…+anxn+b = 0
- Here x1….,xn are variables (these are unknown values), and a1,…, an are the coefficients of the variables (these are real numbers)
- The highest,, power of the variable is one and so-called one-degree equation
- a1…an≠0
Linear Equation
Representation of linear equation with one and two variables:

What do you mean by a solution to a Linear equation?
The solution to a linear equation refers to the values of the variables when substituted in the equation retains the equality of the equation or in other words makes the equation true. A solution to a system of equations is obtained when two lines intersect, i.e. they have the same x and y at one moment in time.
What are the systems of a linear equation?
When two or more equations represent, one situation is called a system of linear equations.
The systems to a linear equation can be
- One/Unique solution
- No solution
- Infinitely Many Solutions


- Unique solution of a linear equation: There is only one value which, when substituted to a variable, makes L.H.S equal R.H.S in the linear equation making the equation true. Linear equation with one variable always has one solution; Eg: 2x=6 wherein x=3 and L.H.S = R.H.S.
Conditions for unique solutions
- Lines in the graph should intersect at one point
- Variables and the numbers should be equal
- The equation should be consistent
- There should be no linear dependency between the equations, i.e. equations should be independent (a1/a2 should not be equal to b1/b2)
- No solution of a linear equation: No value that can be substituted to the variable to make the equation true, i.e. L.H.S will never be equal to R.H.S.; Eg: 2x+3= 2x + 7, On solving this example, we get 3= 7 which is not true
Conditions for no solutions
- Lines in the graph should be parallel to each other
- Equations should be inconsistent and independent (a1/a2=b1/b2≠c1/c2)
- Infinitely many solutions: If infinite values can be substituted to the variable, the result will be L.H.S = R.H.S, making the equation true.
E.g., 2x+3=x+x+3 solving this, we get 2x=2x, so any different value for x will make the equation true. Infinitely Many Solutions is represented by ∞
Conditions for infinite solutions
- Lines in the graph should coincide
- Pair of linear equations should be consistent and dependent (a1/a2 =b1/b2=c1/c2)
How to solve linear equations
There are three basic methods to solve linear equations. They are:
- Elimination method: In this method, we add or subtract two equations to eliminate one of the variables and solve for the other one. And substitute that value in one of the equations and solve for the second variable.
Let us understand this using equations as example
6x+3y=-8
2x+3y=-4
- First, you need to figure out how to eliminate one of the variables, i.e. in the above example, y variables are the same, so subtract that equation and get rid of it.
- So we get 4x+0y=-4, so x=-1
- Substitute that value into one of the original equations and solve for the second variable, i.e. 6(-1)=3y=-8 so y=-⅔, so the point of intersection is x=-1 and y=-2/3
- Substitution method: consider example (A) x+y=3….(1) and 2x – y=6…..(2)
- Isolate a variable in equation 1 i.e. x=3-y
- Substitute this expression to the second equation, i.e. 2x – y=6 becomes 2 (3-y) – y=6
- Solve for the variable as follows
6-2y-y=6
6-3y=6
divide both the sides by -3 so y=0
- Substitute this value into the original equations and solve
2x-0=6
2x=6
X=3
So the point of intersection we get is y=0 and x=3
- Graphing: When both variables are written in slope-intercept form, we use graphing method. In the case of an infinite solution, equations hanging the same graph, the system will be consistent and have an infinite number of solutions as the systems are equivalent, so the equations of this case are dependent.
- Graph the Cartesian plane x and y-axis
- Use equation y (slope-intercept)=mx+b wherein m is the slope, b is the y-intercept
- Consider example equations x-3y=-6….(1)
y=1/3x+2…(2)
- Suppose if we consider x=0, then applying that in equation (1) gives y=2 by dividing both equations by -3
- And if we consider y=0 then solving for x, we get x=-6
- Now, if we graph this y-intercept of 2 and x-intercept of -6, we get line A
- Second-line B is in slope-intercept form with a form Y= mx+b where b is the y-intercept and m is the slope, so line B has a slope of 1/3 and a Y-intercept of 2, and the slope is 1/3
- So go up one unit and right three units, and you will see this case is on the A-line, which means both lines coincide, showing they have an infinite no of solutions to the equation.

Graphical representation of infinitely many solutions
Examples of solving Equations with Infinite Solutions
- X-2X+3=3-X (equation)
-X+3=3-X
3=3
So infinitely many solutions
- 3(x+1)-5=3x-2 (equation)
3x+3-5=3x-2
3x-2=3x-2
-3x -3x
-2=-2
Infinitely many solutions
- Example of a multi step equation
2x+3(x-4)=2(2x-6)+x (equation)
2x+3x-12=4x-12+x
5x-12=5x-12
+12 +12
5x=5x
-5x -5
0=0
Infinitely many solutions
Conclusion
This article clarifies the concepts of linear equations, types and systems in linear equations and how to solve them in simple ways with infinitely many solutions as main examples.





